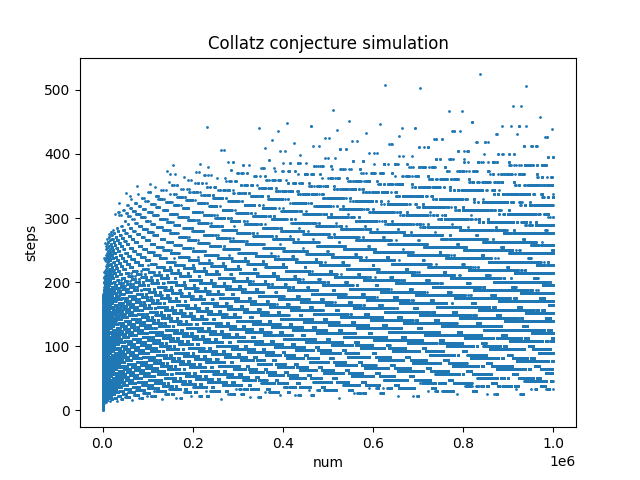
一些 Python 模拟角谷猜想的性能测试
公共部分 def solve(n): step = 0 while n != 1: if n % 2 == 0: n //= 2 else: n = 3 * n + 1 step += 1 return stepN = 1000000 v1 没啥好说的 顺序求解 主要代码： x = [i for i in range(1, N + 1)]y = list(map(solve, x)) v2 测试电脑为 6C12T 故采用max_workers=12 主要代码： from concurrent.futures import ThreadPoolExecutorx = [i for i in range(1, N + 1)]with ThreadPoolExecutor(max_workers=12) as e: y = list(e.map(solve, x)) v3 主要代码： import numpy as npx = np.arange(1, N + 1, 1)y =...
数学随笔
在学校玩计算器时无意发现一个神奇的式子 tan(sin−1(x))→xtan(sin^{-1}(x))\rarr x tan(sin−1(x))→x 当 xxx 初始值为 110\frac{1}{10}101 时 按上面的式子迭代 19 次会得到 19\frac{1}{9}91 再继续迭代 17 次会得到 18\frac{1}{8}81；以此类推 最终到 1 简单整理一下 定义 an+1=an1−an2 (n∈Z)a_{n+1}=\frac{a_n}{\sqrt{1-a_n^2}}\space(n\in\Z) an+1=1−an2an (n∈Z) 若 ai=1k (i∈Z,k∈Z∩[2,+∞))a_i=\frac{1}{k}\space(i\in\Z,k\in\Z\cap[2,+\infin))ai=k1 (i∈Z,k∈Z∩[2,+∞)) 则 ai+2k−1=1k−1a_{i+2k-1}=\frac{1}{k-1}ai+2k−1=k−11 显然只要将表达式代入自身 19 次就能看出端倪了 但由于我计算力低下且在学校...
【解决方案】FFmpeg 推流速度过快
FFmpeg 使用视频源进行推流时，处理速度往往会快于实际帧率，而默认设置下处理完了一段就直接上传，因此速度会过快 解决方法：使用-re参数 ref: https://stackoverflow.com/questions/48479141/understanding-ffmpeg-re-parameter It’s useful for real-time output when ffmpeg is able to process a source at a speed faster than real-time. In that scenario, ffmpeg may send output at that faster rate and the receiver may not be able to or want to buffer and queue its input.
OJ 答案
为造福同学 将 OJ 中 Python 课程答案公布于此 OJ 网址：https://oj.nsfz.net 章节 1：输入、输出及赋值 1120 nsfz 欢迎你 print('nsfz')print('欢迎你') 1381 你的名字 name = input()print('你好', name) 1119 A + B 问题 a = int(input())b = int(input())print(a + b) 章节 2：顺序结构 1003 混合运算 a, b=map(int, input().split())print((a + b) * (a - b)) 1001 求一个数的立方 a = int(input())print(a ** 3) 1008 求长方形面积和周长 a, b = map(int, input().split())print(a * b, (a + b) * 2) 1122 计算线段长度 x1, y1 = map(int, input().split())x2, y2 = map(int, input().split())distance = ((x1 ...
用 Windows To Go 解救机房被机械硬盘拖慢速度的电脑
社团课上找到机房电脑缓慢的根源了 —— 硬盘 有同学带了块移动固态硬盘 并成功从外接 USB 盘启动了电脑 速度直接起飞 机房电脑 CPU 是 10 代 i3 理论上性能不差 但是被 1TB 的希捷机械盘极大地拖慢了速度 于是立刻买了块新固态硬盘准备装系统带机房去用 本来打算整个 118GB 的傲腾装系统的 那样速度肯定更起飞 但是要 500 多块钱 实在太贵了（ 后来还是决定买个便宜的 SATA 硬盘盒加硬盘一共 100 到手 上午买的下午就到了（京东就是快啊） 买的是 128GB 的长城 GW560（买的时候小脑烧了都没看颗粒和 TBW 后来发现是 TLC 就放心了 有 80TBW 按比例来看比 1TB 600TBW 还高一点（） 硬盘盒是个不知名的 支持 SATA3.0 到手后按照标准流程格成 NTFS 先测个性能再说 测试结果： ------------------------------------------------------------------------------CrystalDiskMark 8.0.4 Shizuku Edition x64 (C)...
学校 OJ 探索
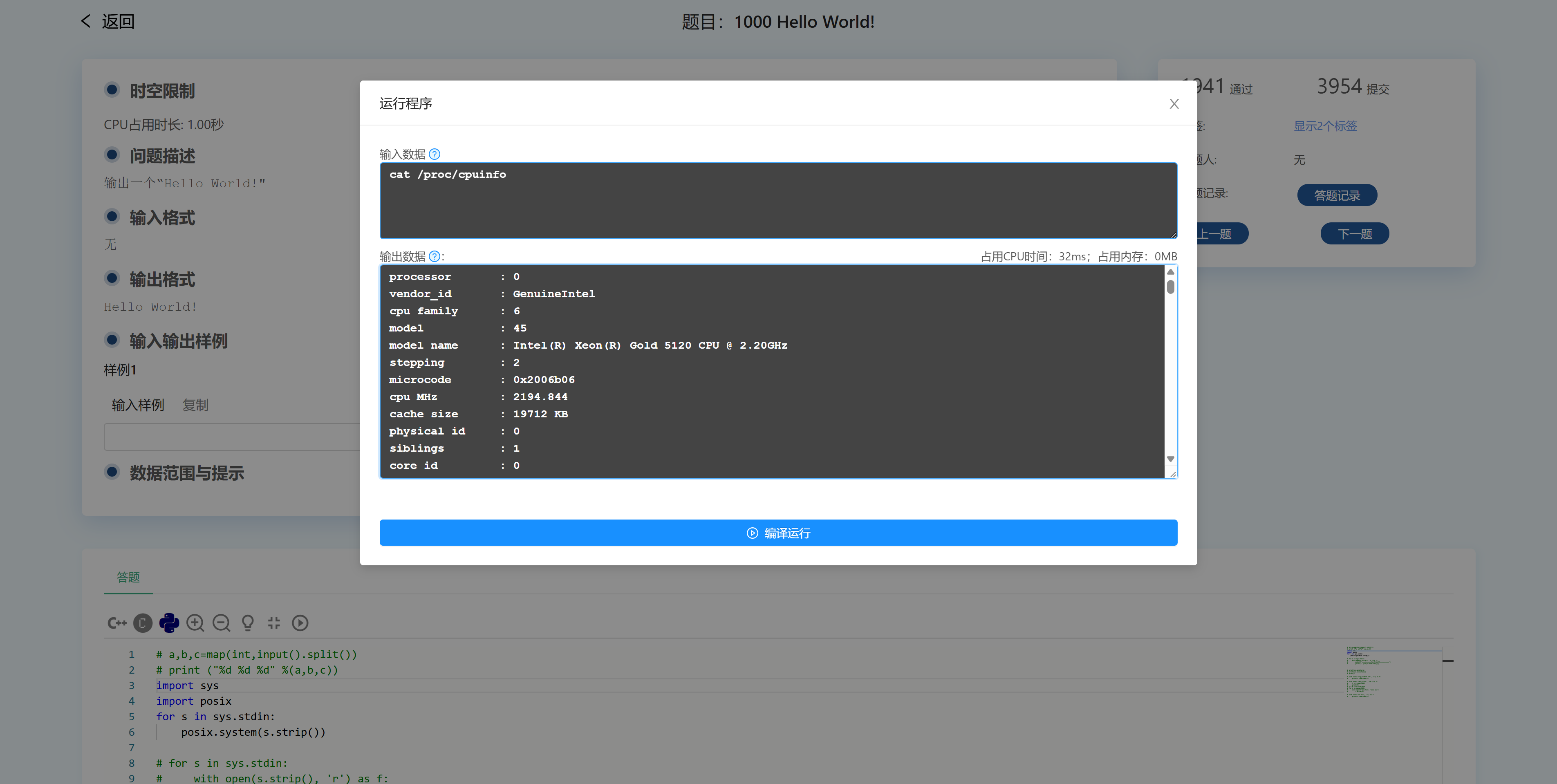
社团课上与同学玩学校 OJ 并尝试对评测机进行一些探索 为了方便就用 python 代码了 已知学校 OJ 使用的是氦星人系统 评测机禁用了os模块 导致一开始没法进行系统调用 遂尝试读写文件 发现居然是可以的 （socket模块依赖os模块 导致暂时只能通过 OJ 的测试功能获取代码输出） 先尝试硬写大量数据以搞爆评测机 发现会报File too large错误 于是放弃 根据平时使用经验（做题时的报错）得知评测机为Linux系统 使用 Python3.8 然后尝试向/tmp目录写文件 发现可以持久化保存 并且另一位同学也能读取到（顺便根据多次实验发现能读取到的概率大约 50% 推测有两个评测机负载均衡） 之后尝试读取/proc等以获取系统信息 如下 信息 来源 值 CPU /proc/cpuinfo Intel® Xeon® Gold 5120 CPU @ 2.20GHz 内存 /proc/meminfo 16GB 硬盘分区 /proc/partitions 104857600 blocks (sda)… （按 1KB / block 则为 100GB）...
一些定积分的几何意义及计算
定积分 一重积分 ∫abf(x)dx\int_{a}^{b}f(x)dx ∫abf(x)dx 几何意义：曲线 f(x)f(x)f(x) 与 xxx 轴围成的曲边梯形的有向面积 物理意义：以 f(x)f(x)f(x) 为线密度函数的曲线在 [a,b][a,b][a,b] 上的质量 计算时可使用牛顿 - 莱布尼茨公式 ∫abf(x)dx=F(b)−F(a)\int_{a}^{b}f(x)dx=F(b)-F(a) ∫abf(x)dx=F(b)−F(a) 其中 F(x)F(x)F(x) 为 f(x)f(x)f(x) 的原函数，即 F′(x)=f(x)F'(x)=f(x)F′(x)=f(x) 二重积分 ∬Df(x,y)dσ\iint_{D}f(x,y)d\sigma ∬Df(x,y)dσ 几何意义：曲面 f(x,y)f(x,y)f(x,y) 与 xyxyxy 平面围成的柱体的有向面积 物理意义： 以 f(x,y)f(x,y)f(x,y) 为面密度函数的平面在区域 DDD 上的质量 以 f(x,y)f(x,y)f(x,y) 为压强函数的平面在区域 DDD 上受到的压力 计算时可在平...
C++ 编译期计算的探索
先放个代码在这 解释下次再说吧（摸了 #include <iostream>#include <utility>#include <array>namespace compiling {#define DEF_BINARY_OP(NAME, OP)\ template <auto N1, auto N2>\ struct NAME##_t : std::bool_constant<N1 == N2> {};\ template <auto N1, auto N2>\ constexpr auto NAME##_v = NAME##_t<N1, N2>::value; DEF_BINARY_OP(less_than, <) DEF_BINARY_OP(less_than_or_equals, <=) DEF_BINARY_OP(greater_than, >) DEF_BINARY_OP(greater_than_or_equals,...
Powershell 美化
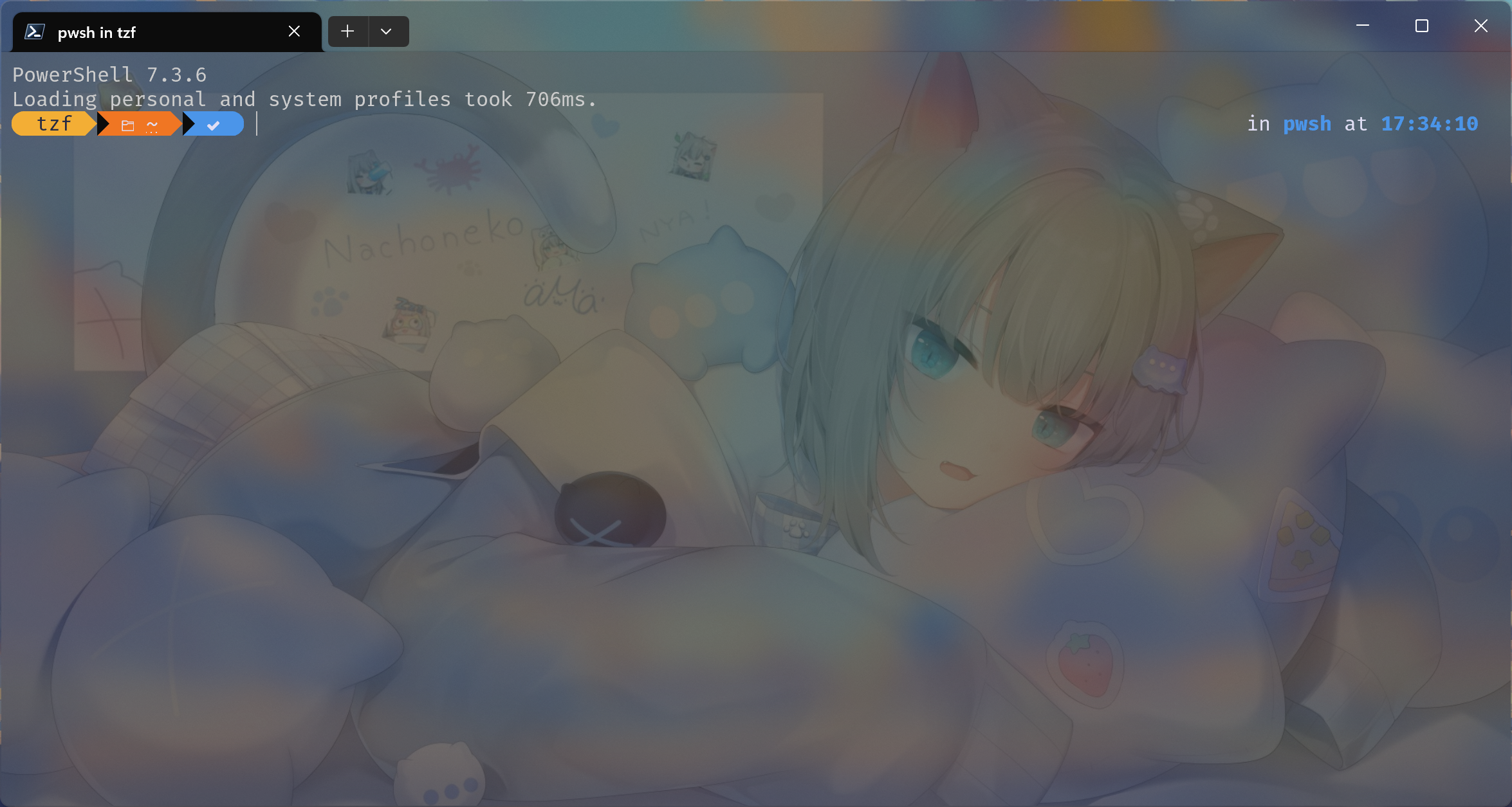
最近看了 B 站的一个视频 受到启发 准备给电脑终端美化一下 因为我把Windows Terminal作为终端默认程序 所以和窗口相关的就不用刻意美化了（本来就很好看） 安装Oh My Posh 跟着官网的教程走就可以了 非常简单 winget install JanDeDobbeleer.OhMyPosh -s winget 之后一定要重启一下终端来加载环境变量 PATH 然后我们会发现终端开始的信息成了这样 显然是字体出了问题 安装字体 这里推荐Nerd Fonts 这是将各种图标符号整合到常用代码字体的一个项目 到下载页面选择一个喜欢的字体用就可以了（这里使用 JetBrainsMono Nerd Font） 安装好后从Windows Terminal的设置页面选择刚才的字体就可以了 终端适配 在终端中打开 PROFILE 文件 code $PROFILE 把下面的内容复制进去 oh-my-posh init pwsh | Invoke-Expression 然后保存 VSCode 适配 修改 VSCode 的settings.json中terminal.integra...
CSharp 随笔 - 癫疯之作
起因是写了这样一段代码 if (e.Action == System.Collections.Specialized.NotifyCollectionChangedAction.Add){ string ipString = string.Join("，", e.NewItems.Cast<IWebSocketConnection>().Select(x => x.ConnectionInfo.ClientIpAddress)); WeakReferenceMessenger.Default.Send<DisplayAlertMessage>(new("有新用户连接", ipString));}else if (e.Action == System.Collections.Specialized.NotifyCollectionChangedAction.Remove){ string ipString = string.Join("，", e.OldItems.Cast<IWebSocketConnection>()....